- Sabemos que la Lógica Tradicional presentaba cuatro tipos fundamentales de enunciado.
- Desde tiempos de Aristóteles, interesó examinar ciertas relaciones lógicas existentes entre estos cuatro tipos de enunciados. Asi, se preguntaba Aristóteles en su obra Liber de Interpretatione : ¿Es posible que sean verdaderos a la vez un enunciado universal afirmativo y un enunciado universal negativo que tengan los mismos predicados?.
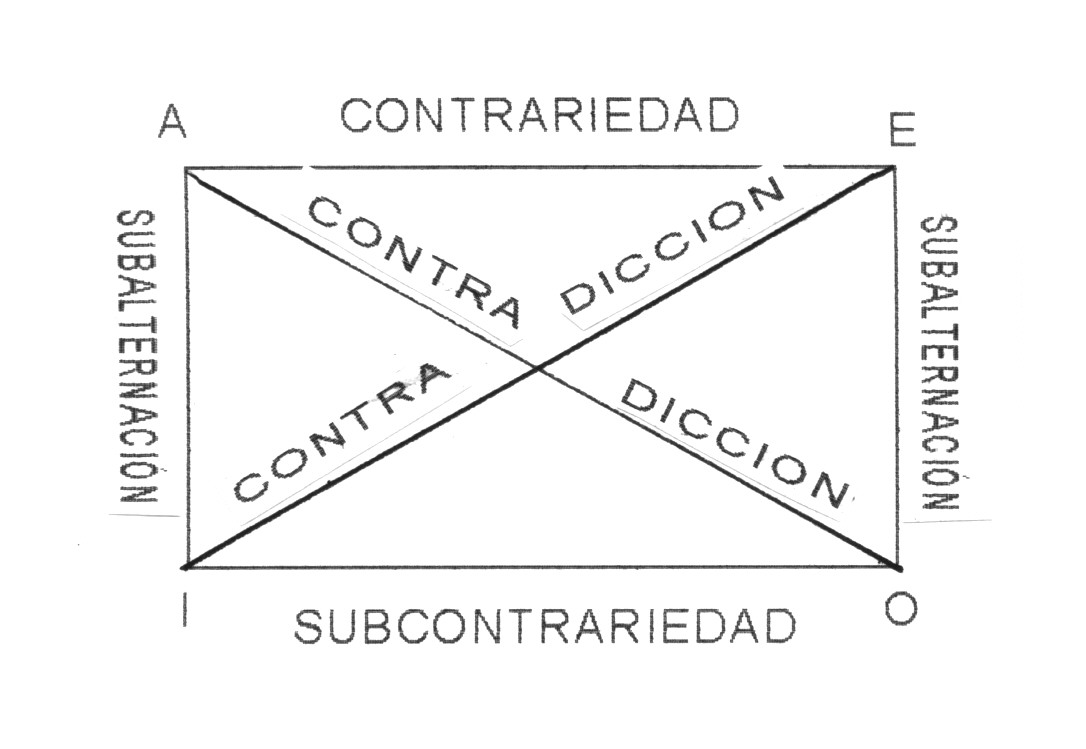
- Aristóteles y la Tradición elaboraron un Cuadro en el que quedaron reflejadas las relaciones entre estos 4 modelos básicos de enunciado.
- UNIVERSALES AFIRMATIVOS:"x (Hx ® Mx):[Para todos los x (Si x es un hombre, entonces x es mortal]
- UNIVERSALES NEGATIVOS: "x (Hx ® ¬Nx) [Para todo x (si x es habitante de Neptuno, entonces de ningún modo puede ser neurótico]
- PARTICULARES AFIRMATIVOS:$x (Px Ù Qx)= [Hay algunos x tal que (son, a la vez, P y Q]
- PARTICULARES NEGATIVOS:$x (Px Ù ¬ Qx)= [Hay algunos x tal que (son P y, sin embargo, no son Q, es decir, no son a la vez, P y Q]
- Contradicción (O-A)
- Contradicción (E-I)
- Contradicción (I-E)
- Subalternación (A-I) + (E-O)
- Contrariedad (A-E)
- Subcontrariedad (I-O)
Cuadro
RELACIONES DE CONTRADICCIÓN [A-O]
- Las relaciones de Contradicción se producen entre las Proposiciones Universales afirmativas (A) y las Proposiciones particulares negativas (O); asi como entre las Proposiciones Universales negativas (E) y las Proposiciones particulares afirmativas (I).
- Parece evidente que un enunciado de tipo A es contradictorio con un enunciado de tipo O. Es decir, si afirmamos que es verdad que Para todo x (Si x es hombre entonces x es mortal), es decir:
"x (Px ® Qx) sería contradictorio afirmar que tambien es verdad que Para algun x (x es hombre y no es mortal), es decir$x (Px Ù ¬Qx) - Ahora bien,¿cómo podemos demostrar que efectivamente las proposiciones de tipo A y las proposiciones de tipo O son contradictorias?
- Para llevar a cabo tal demostración, seguiremos los pasos siguientes:
- Negar la Universal afirmativa (A) de la cual queremos mostrar su contradictoria (O).
- Si partiendo de tal negación llegamos a demostrar que de ella se deriva la contradictoria de la Universal afirmativa, ello significa que la negación de Universal afirmativa (A) nos lleva a algo que tiene que ser contradictorio con la afirmación de tal Universal afirmativa (A).
- Pues bien, consideremos el enunciado siguiente:
Todos los hombres son filósofos
- Si formalizamos el enunciado nos encontramos con:
"x (Hx ® Mx) - Si lo negamos, tenemos:
Ø "x (Hx ® Mx) - Ahora bien, sabemos que:
Ø "x Equivale a:$x Ø - Por lo tanto:
Ø "x (Hx ® Mx) Podría transformarse en:$x Ø (Hx ® Mx) - Ahora bien, si al enunciado:
$x Ø (Hx ® Mx) Le hacemos desaparecer el prefijo cuantificacional:$x Nos encontramos con el enunciado condicional:¬ (Hx ® Mx - Ahora bien, sabemos que:
¬(Hx ® Mx) Puede ser transformado por la regla de la Def ® en la expresión siguiente:(Hx Ù ¬ Mx) - Pues bien si añadimos de nuevo el prefijo cuantificacional que, por estrategia, anteriormente habíamos suprimido, nos encontramos con la expresión:
$x (Hx Ù ¬ Mx) - Lo que sucede es que esta expresión es precisamente la contradictoria de la Universal Afirmativa de la que partimos al principio. Por lo tanto, dado que de la negación de la Universal afirmativa se sigue la contradictoria de tal Universal afirmativa, es evidente que tiene que ser su contradictoria.
- En definiva, hemos demostrado que:
Ø "x (Hx ® Mx) « $x (Hx Ù ¬ Mx) - No olvidar que la particular negativa (O) la hemos derivado a partir de la negación de la universal afirmativa, lo que implica que si se deriva de tal negación es imposible que pudiera derivarse de la afirmación de la universal afirmativa (A) y, por ello, tal particular negativa (O) es su contradictoria.
Relaciones de Oposición
RELACIONES DE CONTRADICCIÓN [O-A]
- Las relaciones de Contradicción se producen entre las Proposiciones Universales afirmativas (A) y las Proposiciones particulares negativas (O); asi como entre las Proposiciones Universales negativas (E) y las Proposiciones particulares afirmativas (I).
- Parece evidente que un enunciado de tipo O es contradictorio con un enunciado de tipo A. Es decir, si afirmamos que es verdad que Para algun x (x es hombre y no es mortal), es decir:
$x (Px Ù ¬Qx) Sería, a su vez, contradictorio afirmar que Para todo x (Si x es hombre entonces x es mortal), es decir:"x (Px ® Qx) - Ahora bien,¿cómo podemos demostrar que efectivamente las proposiciones de tipo O y las proposiciones de tipo A son contradictorias?
- Para llevar a cabo tal demostración, seguiremos los pasos siguientes:
- Negar la Particular negativa (O) de la cual queremos mostrar su contradictoria (A).
- Si partiendo de tal negación llegamos a demostrar que de ella se deriva la contradictoria de la Particular negativa, ello significa que la negación de Particular negativa (O) nos lleva a algo que tiene que ser contradictorio con tal Particular negativa (A) afirmada.
- Pues bien, consideremos el enunciado siguiente:
Algunas cosas dichas metaforicamente no son confusas
- Si formalizamos el enunciado nos encontramos con:
$x (Mx Ù Ø Cx) - Si lo negamos, tenemos:
Ø $x (Mx Ù Ø Cx) - Es decir:
"No hay ninguna x tal que x sea una cosa dicha metaforicamente y x no sea una cosa confusa". - Ahora bien, sabemos que:
Ø $x Equivale a:"x Ø - Por lo tanto:
Ø $x (Mx Ù ¬Cx) Podría transformarse en:"x Ø (Mx Ù ¬ Cx) - Ahora bien, si al enunciado:
"x Ø (Mx Ù ¬ Cx) Le hacemos desaparecer el prefijo cuantificacional:"x Nos encontramos con el enunciado :¬ (Mx Ù ¬ Cx - Ahora bien, sabemos que:
¬(Mx Ù ¬ Cx) Puede ser transformado por la regla de la Def ® en la expresión siguiente:(Mx ® Cx) - Pues bien si añadimos de nuevo el prefijo cuantificacional que, por estrategia, anteriormente habíamos suprimido, nos encontramos con la expresión:
"x (Mx ® Cx) - Lo que sucede es que esta expresión es precisamente la contradictoria de la Particular negativa (O) de la que partimos al principio. Por lo tanto, dado que de la negación de la Particular negativa se sigue la contradictoria de tal Particular negativa, es evidente que tiene que ser su contradictoria.
- En definiva, hemos demostrado que:
Ø $x (Mx Ù ¬ Cx) « "x (Mx ® Cx) - No olvidar que la Universal afirmativa (A) la hemos derivado a partir de la negación de la particular negativa, (O) lo que implica que si se deriva de tal negación es imposible que pudiera derivarse de la afirmación de la Particular negativa (O) y, por ello, tal Universal afirmativa (A) es su contradictoria.
Relaciones de Oposición
RELACIONES DE CONTRADICCIÓN [E-I]
- Las relaciones de Contradicción se producen entre las Proposiciones Universales afirmativas (A) y las Proposiciones particulares negativas (O); asi como entre las Proposiciones Universales negativas (E) y las Proposiciones particulares afirmativas (I).
- Parece evidente que un enunciado de tipo E es contradictorio con un enunciado de tipo I. Es decir, si afirmamos que es verdad que Para ningún x (si x es hombre entonces x no es mortal), es decir:
"x (Px ® ¬Qx) Sería, a su vez, contradictorio afirmar que Para algún x ( x es hombre y x es mortal), es decir:$x (Px Ù Qx) - Ahora bien,¿cómo podemos demostrar que efectivamente las proposiciones de tipo E y las proposiciones de tipo I son contradictorias?
- Para llevar a cabo tal demostración, seguiremos los pasos siguientes:
- Negar la Universal negativa (E) de la cual queremos mostrar su contradictoria (I).
- Si partiendo de tal negación llegamos a demostrar que de ella se deriva la contradictoria de la Universal negativa, ello significa que la negación de la Universal negativa (E) nos lleva a algo que tiene que ser contradictorio con tal Universal negativa (E) afirmada.
- Pues bien, consideremos el enunciado siguiente:
Ningún Jefe se equivoca
- Si formalizamos el enunciado nos encontramos con:
"x (Jx ® Ø Ex) - Es decir:
"Para todo x (Si x es un jefe entonces x no se equivoca)". - Si lo negamos, tenemos:
Ø "x (Jx ® Ø Ex) - Ahora bien, sabemos que:
Ø "x Equivale a:"x Ø - Por lo tanto:
Ø "x (Jx ® ¬ Ex) Podría transformarse en:$x Ø (Jx ® ¬ Ex) - Ahora bien, si al enunciado:
$x Ø (Jx ® ¬ Ex) Le hacemos desaparecer el prefijo cuantificacional:$x Nos encontramos con el enunciado :¬ (Jx ® ¬ Ex - Ahora bien, sabemos que:
¬(Jx ® ¬ Ex) Puede ser transformado por la regla de la Def ® en la expresión siguiente:(Ø Ø) Jx Ù Ø Ø Ex) - Pues bien si añadimos de nuevo el prefijo cuantificacional que, por estrategia, anteriormente habíamos suprimido, nos encontramos, despues de aplicar la DN, con la expresión:
$x (Jx Ù Ex) - Lo que sucede es que esta expresión es precisamente la contradictoria de la Universal negativa (E) de la que partimos al principio. Por lo tanto, dado que de la negación de la Universal negativa se sigue la contradictoria de tal Universal negativa, es evidente que tiene que ser su contradictoria.
- En definiva, hemos demostrado que:
Ø ["x (Jx ® ¬ Ex)] « $x (Jx Ù Ex) - No olvidar que la Particular afirmativa (I) la hemos derivado a partir de la negación de la Universal negativa, (E) lo que implica que si se deriva de tal negación es imposible que pudiera derivarse de la afirmación de la Universal negativa (E) y, por ello, tal Particular afirmativa (A) es su contradictoria.
Relaciones de Oposición
RELACIONES DE CONTRADICCIÓN [I-E]
- Las relaciones de Contradicción se producen entre las Proposiciones Universales afirmativas (A) y las Proposiciones particulares negativas (O); asi como entre las Proposiciones Universales negativas (E) y las Proposiciones particulares afirmativas (I).
- Parece evidente que un enunciado de tipo I es contradictorio con un enunciado de tipo E. Es decir, si afirmamos que es verdad que Para algún x (x es hombre y x es mortal), es decir:
$x (Px Ù Qx) Sería, a su vez, contradictorio afirmar que Para todo x (si x es un hombre entonces x no es mortal), es decir:"x (Px ® ¬ Qx) - Ahora bien,¿cómo podemos demostrar que efectivamente las proposiciones de tipo I y las proposiciones de tipo E son contradictorias?
- Para llevar a cabo tal demostración, seguiremos los pasos siguientes:
- Negar la Particular afirmativa (I) de la cual queremos mostrar su contradictoria (E).
- Si partiendo de tal negación llegamos a demostrar que de ella se deriva la contradictoria de la Particular afirmativa, ello significa que la negación de la Particular afirmativa (I) nos lleva a algo que tiene que ser contradictorio con tal Particular afirmativa (I) afirmada.
- Pues bien, consideremos el enunciado siguiente:
Algunos lingüistas creen que la sintaxis es autónima.
- Si formalizamos el enunciado nos encontramos con:
$x (Lx Ù Cx) - Es decir:
"Para algún x (x es un lingüista y x cree que la sintaxis es autónima)". - Si lo negamos, tenemos:
Ø $x (Lx Ù Ex) - Ahora bien, sabemos que:
Ø $x Equivale a:"x Ø - Por lo tanto:
Ø $x (Lx Ù Cx) Podría transformarse en:"x Ø (Lx Ù Cx) - Ahora bien, si al enunciado:
"x Ø (Lx Ù Cx) Le hacemos desaparecer el prefijo cuantificacional:"x Nos encontramos con el enunciado :Ø (Lx Ù Cx) - Ahora bien, sabemos que:
Ø (Lx Ù Cx Puede ser transformado por la Ley de Morgan en:(Ø Lx Ú Ø Cx) - Y a su vez, la expresión anterior pueden transformarse por la regla
de la Def ®
en la expresión siguiente:
(Lx ® Ø Cx) - Pues bien si añadimos de nuevo el prefijo cuantificacional que, por estrategia, anteriormente habíamos suprimido, nos encontramos, despues de aplicar la DN, con la expresión:
"x (Lx ® Ø Cx) - Lo que sucede es que esta expresión es precisamente la contradictoria de la Particular afirmativa (I) de la que partimos al principio. Por lo tanto, dado que de la negación de la Particular afirmativa se sigue la contradictoria de tal Particular afirmativa, es evidente que tiene que ser su contradictoria.
- En definiva, hemos demostrado que:
Ø [$x (Lx Ù Cx)] « "x (Lx ® ¬ Cx) - No olvidar que la Universal negativa (E) la hemos derivado a partir de la negación de la Particular afirmativa, (I) lo que implica que si se deriva de tal negación es imposible que pudiera derivarse de la afirmación de la Particular afirmativa (I) y, por ello, tal Universal negativa (E) es su contradictoria.
Relaciones de Oposición
RELACIONES DE SUBALTERNACIÓN [A-I][E-O]
- Las relaciones de Subalternación se producen entre las Proposiciones Universales afirmativas (A) y las Proposiciones particulares afirmativas (I); asi como entre las Proposiciones Universales negativas (E) y las Proposiciones particulares afirmativas (O)
- Según la Lógica Tradicional, las relaciones de verdad entre los enunciados subalternos son las siguientes:
- Si un enunciado universal afirmativo ["x (Px)] es verdadero, entonces será tambien verdadero el enunciado particular afirmativo [$x (Px)]
- De igual modo, si es verdadero el enunciado universal negativo ["x (¬Px)]tambien será verdadero el enunciado particular negativo [$x (¬Px)]
- Ahora bien, estos dos esquemas solamente serán válidos en el caso de que se excluyan los universos vacíos del discurso. Algo que no sucede, por ejemplo, en los Diagramas de Venn
- Sin embargo, según la Lógica de Predicados moderna las Relaciones de Subalternación no se cumplen. [Para saber porque, puede seguirse el mismo método que hemos seguido para averigüar como las relaciones de contradicción presentes en el cuadro tradicional si se cumplen según la Lógica de Predicados].
- Por lo tanto, en las relaciones de Subalternación, según la Lógica de Predicados, de la verdad de:
"x (Px ® Qx) no puede inferirse:$x (Px Ù Qx) Como tampoco la verdad de:$x (Px Ù ¬ Qx) se puede derivar a partir de:"x (Px ® ¬ Qx)
Relaciones de Oposición
RELACIONES DE CONTRARIEDAD [A-E]
- Las relaciones de Contrariedad se producen entre las Proposiciones Universales afirmativas (A) y las Proposiciones Universales negativas (E).
- Pues bien, la Lógica de predicados tampoco admite tal relación. Y es que, como vimos al analizar la relación de contrariedad entre los Esquemas Simples, vimos que tales esquemas podían fundamentarse en los de Subalternación. Pero estos no se cumplen ahora. Por lo tanto las relaciones de contraruiedad tampoco se cumplen
- Las Relaciones de Contrariedad, según la Lógica de Predicados, se pueden formalizar del modo siguiente:
"x (Px ® Qx) ® Ø ["x (Px ® Ø Qx)] Asi como:"x (Px ® Ø Qx) ® Ø ["x (Px ® Qx)] - Notar que los consecuentes de ambos condicionales equivalen, a partir de las deducciones realizadas en las relaciones de contradicción de caracter simple, a lo siguiente:
Primer consecuente: Ø ["x (Px ® Ø Qx)] Equivale a: $x (Px Ù Qx) Segundo consecuente: Ø ["x (Px ® Qx)] Equivale a: $x (Px Ù ¬ Qx) - Ahora bien, si admitieramos esta relación, deberíamos admitir tambien la de subalternación.
Relaciones de Oposición
RELACIONES DE SUBCONTRARIEDAD [I-O]
- Las relaciones de Subcontrariedad se producen entre las Proposiciones Particulares afirmativas (I) y las Proposiciones Particulares negativas (O).
- Pues bien, la Lógica de predicados tampoco admite tal relación. De ella puede decirse lo mismo que lo dicho sobre las relaciones de contrariedad.
- Las Relaciones de Subcontrariedad, según la Lógica de Predicados, se pueden formalizar del modo siguiente:
Ø $x (Px Ù Qx) ® $x (Px Ù Ø Qx)] Asi como:Ø $x (Px Ù Ø Qx) ® $x (Px Ù Qx) - Notar que los antecedentes de ambos condicionales equivalen, a partir de las deducciones realizadas en las relaciones de contradicción de caracter simple, a lo siguiente:
Primer antecedente: Ø $x (Px Ù Qx) Equivale a: "x (Px ® ¬ Qx) Segundo antecedente: Ø $x (Px Ù ¬ Qx)] Equivale a: "x (Px ® Qx) - Ahora bien, si admitieramos esta relación, deberíamos admitir tambien la de subalternación.
Relaciones de Oposición
Tradicional y Predicados
Tradicional y Cuadro
Existen cuatro tipos de relación entre los enunciados A,E,I,O: