- Sabemos que en Lógica de Clases cabe distinguir cuatro tipos fundamentales de enunciado.
- Desde tiempos de Aristóteles, interesó examinar ciertas relaciones lógicas existentes entre estos cuatro tipos de enunciados. Asi, se preguntaba Aristóteles en su obra Liber de Interpretatione : ¿Es posible que sean verdaderos a la vez un enunciado universal afirmativo y un enunciado universal negativo que tengan los mismos predicados?.
- Aristóteles y la Tradición elaboraron un Cuadro en el que quedaron reflejadas las relaciones entre estos 4 modelos básicos de enunciado.
- Pasaremos a analizar tal Cuadro, aunque señalando el siguiente matiz: tradicionalmente se consideraba que las 4 formas más simples de enunciados eran los predicados monádicos siguientes:
Todo S es P (A) Ningún S es P (E) Algún S es P (I) Algún S no es P(O)
- De todos modos, en la Lógica del Predicados actúal se considera que existen 4 formas todavía más Simples que las anteriores.
- UNIVERSALES AFIRMATIVOS:"x (Hx ® Mx):[Para todos los x (Si x es un hombre, entonces x es mortal]
- UNIVERSALES NEGATIVOS: "x (Hx ® ¬Nx) [Para todo x (si x es habitante de Neptuno, entonces de ningún modo puede ser neurótico]
- PARTICULARES AFIRMATIVOS:$x (Px Ù Qx)= [Hay algunos x tal que (son, a la vez, P y Q]
- PARTICULARES NEGATIVOS:$x (Px Ù ¬ Qx)= [Hay algunos x tal que (son P y, sin embargo, no son Q, es decir, no son a la vez, P y Q]
- Universales afirmativos:Todos los x son P ["x (Px)]
- Universales negativos:Ningún x es P (todo x es no-p) ["x (¬Px)]
- Particulares afirmativos:Algún x es P [$x (Px)]
- Particulares negativos:Algún x no es P (algún x es no-p) [$x (¬Px)]
- Subalternación
- Contrariedad
- Subcontrariedad
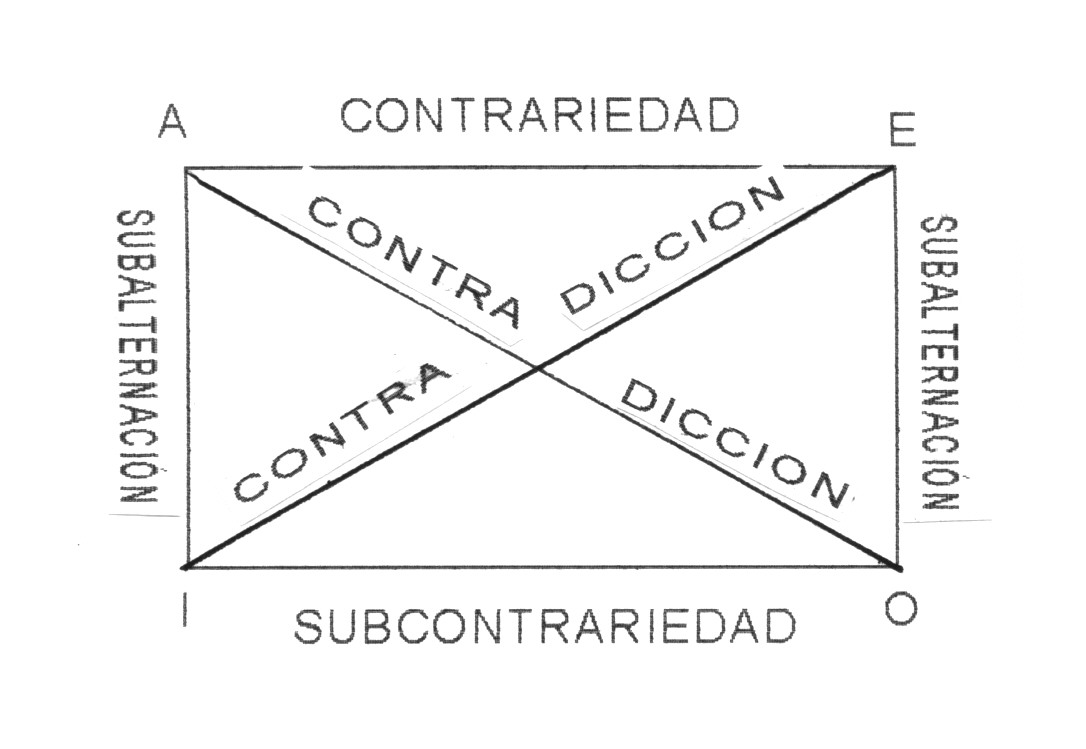
Cuadro
RELACIONES DE CONTRADICCIÓN [A-O] [E-I]
- Las relaciones de Contradicción se producen entre las Proposiciones Universales afirmativas (A) y las Proposiciones particulares negativas (E); asi como entre las Proposiciones Universales negativas (E) y las Proposiciones particulares afirmativas (I)
- Parece evidente que un enunciado de tipo A es contradictorio con un enunciado de tipo O. Es decir, si afirmamos que es verdad que Todo x es P ["x (Px)] sería contradictorio afirmar que tambien es verdad que Algun x no es P [$x (¬Px)]
- Del mismo modo, parece evidente que un enunciado de tipo E es contradictorio con un enunciado de tipo I. Es decir, si afirmamos que es verdad que Ningún x es P ["x (¬Px)] sería contradictorio afirmar que tambien es verdad que Algún x es P [$x (Px)]
- Debemos tener en cuenta, además, dos cuestiones, en relación con las relaciones de contradicción entre predicados:
- La Relación es simétrica, es decir, que si el enunciado A es contradictorio con el enunciado O, tambien el enunciado O lo es con A. Y del mismo modo, si el enunciado E es contradictorio con el enunciado I, tambien el enunciado I es contradictorio con E.
- Decir que un enunciado es contradictorio de otro es como decir que equivale a la
Predicados y Cuadro
Existen 4 tipos de enunciados predicativos simples:
Predicados y Cuadro
Predicados y Cuadro
Existen cuatro tipos de relación entre los enunciados A,E,I,O:
Relaciones de Oposición
El siguiente esquema nos muestra como un enunciado que es contradictorio de otro equivale a la negación de ese otro:
- Universal afirmativo:Todo x es P ["x (Px)] EQUIVALE a un Particular negativo NEGADO: No es cierto que algún x no es P [Ø $x (¬Px)]
- Universal negativo:Ningún x es P ["x (¬Px)] EQUIVALE a Particular afirmativo NEGADO: No es cierto que algún x es P [Ø $ x (Px)]
- En definitiva:
["x (Px)] « [Ø $x (¬Px)] ["x (¬Px)] « [Ø $x (Px)]
Relaciones Contradiccion
Sabemos que un enunciado que es contradictorio de otro equivale a la negación de ese otro.
Realiza la conversión por equivalencia de negación entre los enunciados siguientes:
- TODO X ES P=["x (Px)]
- ALGÚN X ES P=[$x (Px)]
- NINGÚN X ES P=["x (¬Px)]
- ALGÚN X NO ES P=["x (¬Px)]
Relaciones Contradiccion
Un enunciado que es contradictorio de otro equivale a la negación de ese otro.En este contexto, la conversión a los ejercicios señalados es la siguiente:
Ejercicios Contradicción-Negación
- Las relaciones de
- Si un enunciado universal afirmativo ["x (Px)] es verdadero, entonces será tambien verdadero el enunciado particular afirmativo [$x (Px)]
- De igual modo, si es verdadero el enunciado universal negativo ["x (¬Px)]tambien será verdadero el enunciado particular negativo [$x (¬Px)]
- Ahora bien, estos dos esquemas solamente serán válidos en el caso de que se excluyan los universos vacíos del discurso. Algo que no sucede, por ejemplo, en los Diagramas de Venn
- Por otro lado, si un enunciado particular afirmativo [$x (Px)] es falso, entonces tambien será falso el subalterno A ["x (Px)]. Y si es falso el enunciado particular negativo [$x (¬Px)] tambien sera falso el subalterno E ["x (¬Px)]
- Las relaciones de Subalternación plantean Problemas interesantes de analizar.