COMENTARIO A UNIVERSALES AFIRMATIVAS
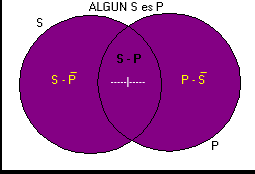
En este Esquema se nos ofrece una doble información acerca del porque Todos los S son P.
El primer tipo de información se centra en la zona de intersección [Negro] de las clases S-P que está vacía. Si no estuviera vacía, esta zona representaría a los individuos que son S y no son P.
Ahora bien, al estar vacía, nos está diciendo que carece de sujetos que son S y no son P. En esa zona, por tanto, no existe ningún individuo que sea S y que no sea P. En lógica de Predicados si simbolizaría así:
Ø
$x
(Sx Ù
ØPx)
El segundo tipo de información se centra en la zona de intersección neutra [Violeta] de S-P, de la cual no sabemos si está vacía o no. Esta zona de intersección de las clases S-P, nos permite asegurar, no que hay individuos S que sean P, pero sí que si los hay, entonces serán P; esto es: para todo individuo x, si x es S entonces x es P. En lógica de predicados se simbolizaría así:
"x
(Sx ® Px)
COMENTARIO A UNIVERSALES NEGATIVAS
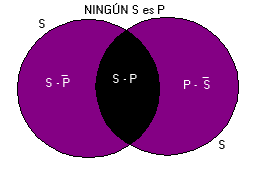
En este Esquema se nos ofrece una doble información acerca del porque Ningún S es P.
El primer tipo de información se centra en la zona de intersección [Negro] de las clases S-P que está vacía. Si no estuviera vacía, esta zona representaría a los individuos que son S y son P.
Ahora bien, al estar vacía, nos está diciendo que carece de sujetos que son S y son P. En esa zona, por tanto, no existe ningún individuo que sea S y que sea P. En lógica de Predicados si simbolizaría así:
Ø
$x
(Sx ÙPx)
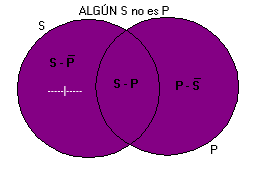
El segundo tipo de información se centra en la zona de no intersección neutra [Violeta] de S, de la cual no sabemos si está vacía o no. Esta zona de intersección de S, nos permite asegurar, no que hay individuos S que no son P, pero sí que si los hay, entonces serán S y no serán P; esto es: para todo individuo x, si x es S entonces x no es P. En lógica de predicados se simbolizaría así:
"x
(Sx ®
Ø Px)