Clases o Conjuntos

LÓGICA DE CLASES o CONJUNTOS

Lógica Proposicional,Predicados y Clases
Introducción Lógica de Clases
Simbolización Lógica de Clases
Conexiones entre clases
Relaciones entre clases

Lógica de Clases

LÓGICA PROPOSICIONAL, LÓGICA DE PREDICADOS Y LÓGICA DE CLASES

En la Lógica Proposicional se considera a los enunciados como unidades atómicas o moleculares que pueden ser V o F. No se concibe a tales enunciados como algo más complejo integrado por un sujeto y un predicado y en donde podrían estudiarse sus relaciones y conexiones.
En la Lógica de Predicados, sin embargo, se considera los enunciados como algo complejo y en donde se afirma de alguien algún tipo de atributo. Así, por ejemplo, si decimos que: "Felipe Gonzáles es un gran pensador político"; o que: "Goebels era cojo", desde el punto de vista de la Lógica proposicional unicamente estaríamos ante dos enunciados atómicos que pueden ser V o F. Para la Lógica de Predicados, sin embargo, habría algo más: en estos enunciados se estaría afirmando que los sujetos de los mismos poseen determinados atributos [ser pensador político, ser cojo].
La Lógica de Clases enfoca el asunto de un modo diferente: en un enunciado en donde exista un Sujeto y un Predicado (por ejemplo: Goebels era cojo) se estaría señalando, no tanto un atributo del sujeto, como la pertenencia del sujeto a una determinada clase. En este caso, se estaría señalando la pertenencia de Goebels a la clase de los hombres cojos.

Conjuntos

INTRODUCCIÓN A LA LÓGICA DE CLASES

Una Clase es un conjunto de individuos que tienen, al menos, una propiedad común, que es la de pertenecer a una determinada Clase. En definitiva, dada una propiedad cualquiera, por ejemplo, la propiedad de ser marxista-leninista o río de Siberia o dios etrusco, es evidente que pertenecerían a cada una de estas clases [conjuntos o colecciones] todas aquellas entidades que reunan tales propiedades. De este modo, surgiría el conjunto o clase de los marxistas leninistas, de los rios de Siberia o de los dioses etruscos.
El Símbolo de pertenencia a una clase es:
e
En este sentido [ x e A ] lo deberíamos leer como:
"x pertenece a la clase A"
En la Lógica de Clases los Predicados se emplean de modo extensional. Es decir, no interesa la comprensión de un predicado (lo que connota) sino unicamente su extensión (lo que denota). Así, en Lógica de clases no interesa saber, por ejemplo, en qué consiste ser filósofo (comprensión o connotación del término) sino únicamente que hay un conjunto de individuos (extensión o denotación del término) que forman la clase de los filósofos y que están en relación con otras clases, por ejemplo, la de los mortales o la de los hombres.
Las Clases son los elementos más simples de la lógica. Ahora bien, las clases no son proposiciones, y, por tanto, no pueden ser verdaderas o falsas. Por ejemplo,la clase de las sirenas, es simplemente vacía, no falsa. Falsa sería si afirmáramos que: "algunas sirenas leen a Platón".
Es posible hacer conexiones entre clases (por ejemplo se podrían unir la clase de los filósofos y la clase de los españoles) Ahora bien, con tal unión solo obtenemos una nueva clase (los filósofos españoles), no una proposición. Lo mismo sucede con el Complemento o negación de pertenencia de una clase a otra. Solamente cuando se establecen relaciones entre clases se obtienen verdaderas proposiciones (por ejemplo, la clase de los filósofos se incluye en la clase de los mortales, que es lo mismo que decir que los filósofos son mortales) en una relación de inclusión de una clase en otra.
Debemos tratar, por tanto, acerca de las conexiones y de las Relaciones de Clases.

Conjuntos

CONEXIONES Y COMPLEMENTO NUEVAS CLASES [Complemento,Intersección,Unión]

La conexión entre clases unicamente permite la aparición de nuevas clases. Se trata, por tanto, de nuevas clases y no de proposiciones o enunciados sobre clases.

CLASE COMPLEMENTARIA: Se simboliza como -A
Supongamos, por ejemplo, la clase de los canallas. (A) Es evidente que pertenecen a ella todas aquellas entidades que ostentan esta propiedad, que merecen este calificativo.
Ahora bien, tambien es evidente que, con respecto a esta clase de canallas, nos podemos imaginar esta otra: la clase formada por todas aquellas entidades que no son unos canallas, es decir, la clase de los no-canallas. [ -A ]
Pues bien, a esta última clase (la que no-es) se le llama Clase Complemento de la primera clase. Por lo tanto la clase complemento de la clase de los canallas (A) es la clase de los no-canallas (-A). EJEMPLOS:La Clase complemento de la clase de las cosas agradables(A) sería la clase de las cosas desagradables (-A)
La Clase complemento de la clase de los suicidas (A) sería la clase formada por todos aquellos que no se han suicidado (-A)
La clase Complemento se simboliza asi: - A
Ver su representación con Círculos.
CLASE INTERSECCIÓN O PRODUCTO:Se simboliza como W
Supongamos que la Clase A es la clase de los gasterópodos. Y que la Clase B es la de los necios. Es evidente que, a base de la clase A y de la Clase B, podemos construir la clase de las cosas que son a la vez A y B: la clase formada por todas aquellas entitades que son a la vez gasterópodos y necios. Dicho sin rodeos: la clase de los gasterópodos necios. Esta nueva clase es el producto de las otras dos y ,por ello, se le llama Clase producto. Producto, a su vez, de la operación de Intersección de clases.
Al igual que la Conjunción de dos enunciados es un enunciado molecular, la Inntersección de dos clases es una Clase nueva cuyas miembros serán todos aquellas entidades que pertenezcan a la vez a una y a otro clase.
EJEMPLO:La intersección de la clase de los enanos y de la clase de los -seres humanos- cariacontecidos será la Clase de los enanos cariacontecidos. Así pues, del mismo modo que una conjunción de enunciados sólo es verdadera cuando lo son todos sus miembros, de una clase producto de dos clases sólo formarán parte aquellas entidades que sean miembros de ambas a la vez. El producto de la intersección de clases A y B, se simboliza así. A W B
Ver su representación con Círculos.
CLASE UNIÓN O SUMA:Se simboliza como: U
Supongamos que la Clase A es la clase de todas aquellas personas que han conseguido mantenerse en el poder por medio del terror, y que la clase B es la clase de todas aquellas personas que han conseguido mantenerse en el poder mediante la corrupción.
Parece evidente que, a base de la clase A y de la clase B, podemos construir la clase de todas aquellas personas que han conseguido mantenerse en el poder o bien mediante el terror, o bien mediante la corrupción, o bien mediante ambos procedimientos.
Para ser miembro de esta clase, resultante de la operación que se denomina Unión o Suma de clases, no hace falta, (al contrario que con la Intersección o Producto) haber utilizado, a la vez, el instrumento de poder del terror y el de la corrupción: basta con haber utilizado uno de esos dos recursos. Aunque tambien, desde luego, formarán parte de la clase Unión quienen hayan echado mano de ambos.
La Unión de clases A y B se simboliza así: A U B
Ver su representación con Círculos.

Conjuntos

COMPLEMENTO,INTERSECCIÓN Y UNIÓN DE CLASES

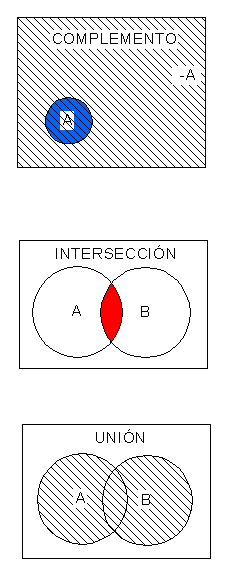
Complemento-Intersección-Unión

COMENTARIO A LAS CLASES COMPLEMENTO,INTERSECCIÓN Y UNIÓN DE CLASES

OBSERVACIONES A LA CLASE COMPLEMENTO: Notar que mientras que la clase A (en el círculo azul) representa a los miembros de una clase determinada, el cuadrado sombreado de - A representaría a la clase de individuos que no pertenecen a la clase A. Por ejemplo, si la Clase A (azul) representara a la clase de los animales racionales, la Clase -A representaría a los animales que no pertenecen a la clase de los animales racionales u hombres.
OBSERVACIONES A LA CLASE INTERSECCIÓN:El color rojo en la zona de intersección entre A y B representa a la clase de individuos que pertenecen a la vez a las clases A y B. Por ejemplo, la expresión "los roedores ibéricos", representaría a la clase de animales que pertenecen simultaneamente a la clase de los roedores y a la clase de la fauna ibérica.
OBSERVACIONES A LA CLASE UNIÓN:Notar que la superficie rayada abarca tanto las zonas de no intersección como la zona de intersección.En este sentido, los círculos representan a la clase de individuos que pertenecen al menos a una de las dos clases, o a ambas a la vez. Por ejemplo, se puede ser de la clase de los terroristas y no corruptos,(A) de la clase de los corruptos pero no terroristas,(B) y de ambas cosas a la vez (zona de intersección A-B)

Gráficos

SIMBOLIZACIÓN EN LOGICA DE CLASES

SIMBOLIZACIÓN

VARIABLES DE CLASE: A, B, C, etc
PERTENENCIA A UNA CLASE: e
x e A se lee: x pertenece a la clase A
x - e A se lee: x no pertenece a la clase A.
COMPLEMENTO DE CLASE: negador: -
-A se lee: "el complemento de A".
CONEXIONES DE CLASE:
- Intersección(o producto): Productor: W
  A W B se lee: Intersección de A y B o A intersección B
- Unión (o suma): sumador: U
  A U B se lee: Unión de A y B o A unión B
RELACIONES DE CLASE:
- Inclusión: Inclusor: C
  A C B se lee A está incluida en B
  A -C B se lee A no está incluida en B
- Igualdad (o equivalencia):Igualador: =
  A = B se lee A es igual a B
  A /= se lee A no es igual a B

Conjuntos

RELACIONES DE CLASES PROPOSICIONES O ENUNCIADOS SOBRE CLASES [Inclusión e Igualdad]

La conexión entre clases unicamente permitía la aparición de nuevas clases, y no de proposiciones o enunciados sobre clases. Mediante las Relaciones de clases se obtienen no nuevas clases, sino proposiciones o enunciados sobre clases (que pueden ser, por tanto, verdaderas o falsas).

INCLUSIÓN DE CLASES: Se simboliza como C
Tomemos dos clases cualesquiera.La clase A podría ser,por ejemplo, la clase de los proletarios con conciencia de clase. Y la clase B podría ser la clase de los proletarios - sin más. Es evidente que la clase B es más amplia que la clase A. Es evidente que la clase B incluye a la clase A. Dicho de otro modo, todos los proletarios con conciencia de clase son proletarios, pero no todos los proletarios son proletarios con conciencia de clase. Dicho todavía de otro modo: todos los miembros de la Clase A son miembros de la Clase B, pero no viceversa. Pues bien, cuando todos los miembros de una clase, por el hecho de serlo, son tambien miembros de otra (aunque no necesariamente a la inversa) se dice que la primera está incluida en la segunda.
La Inclusión de Clases se simboliza asi:
A C B
Ver su representación con Círculos.
IGUALDAD DE CLASES:Se simboliza como: =
Tomemos dos clases cualesquiera. Sea la clase A la clase de los lingüistas rigurosamente científicos, y la clase B la clase de los lingüistas que cultivan la lingüistíca generativo-transformacional. A estas dos clases les ocurre algo. Les ocurre que tienen exactamente los mismos miembros. Y dos clases que tienen los mismos miembros son iguales.
La igualdad de clases se simboliza así: A = B
Ver su representación con Círculos.
Notar que el símbolo " = " no sirve para componer nombres de clases, sino para componer enunciados sobre clases, para decir que tal clase es igual a tal otra.
Ahora bien, no es lo mismo decir que dos clases tiene los mismos miembros (en cuyo caso, lo que estamos diciendo, como acabamos de ver, es decir que ambas clases son iguales, son la misma clase) que decir que tienen el mismo número de miembros , en cuyo caso diremos que son clases equivalentes. Es obvio que si dos clases son iguales son tambien, por fuerza, equivalentes. Pero tambien es obvio que la conversa no es verdadera. La clase formada por los miembros del conjunto The Beatles y la clase formada por los cuatro profetas Mayores son equivalentes, pero distan mucho de ser iguales.

Conjuntos

INCLUSIÓN E IGUALDAD DE CLASES

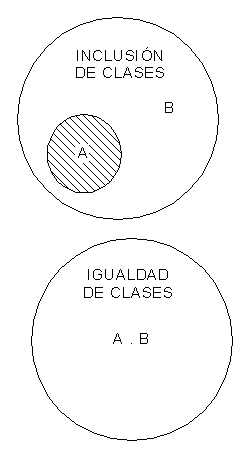
Inclusión-Igualdad

COMENTARIO A LAS CLASES DE INCLUSIÓN E IGUALDAD

OBSERVACIONES A LA CLASE INCLUSIÓN: Observar que el círculo A se encuentra contenido o incluido en el círculo más grande B
OBSERVACIONES A LA CLASE DE IGUALDAD: Observar que el círculo contiene los mismos miembros de la clase A que de la clase B.

Gráficos